文章摘要

Deepseek-v3.2

初探动态规划

动态规划（dynamic programming）是一个重要的算法范式，它将一个问题分解为一系列更小的子问题，并通过存储子问题的解来避免重复计算，从而大幅提升时间效率。

在本节中，我们从一个经典例题入手，先给出它的暴力回溯解法，观察其中包含的重叠子问题，再逐步导出更高效的动态规划解法。

给定一个共有 n 阶的楼梯，你每步可以上 1 阶或者 2 阶，请问有多少种方案可以爬到楼顶？

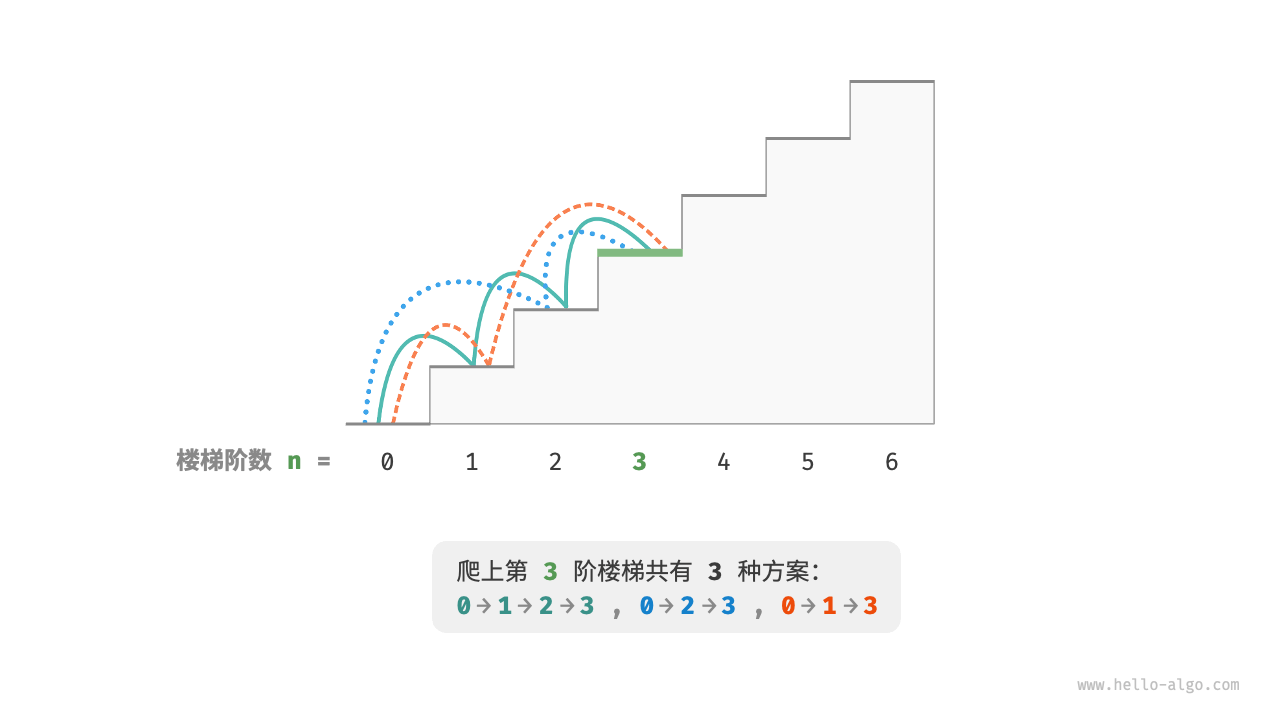
如下图所示，对于一个 3 阶楼梯，共有 3 种方案可以爬到楼顶。

本题的目标是求解方案数量，我们可以考虑通过回溯来穷举所有可能性。具体来说，将爬楼梯想象为一个多轮选择的过程：从地面出发，每轮选择上 1 阶或 2 阶，每当到达楼梯顶部时就将方案数量加 1 ，当越过楼梯顶部时就将其剪枝。代码如下所示：

/* 回溯 */
void backtrack(vector<int> &choices, int state, int n, vector<int> &res) {
    // 当爬到第 n 阶时，方案数量加 1
    if (state == n)
        res[0]++;
    // 遍历所有选择
    for (auto &choice : choices) {
        // 剪枝：不允许越过第 n 阶
        if (state + choice > n)
            continue;
        // 尝试：做出选择，更新状态
        backtrack(choices, state + choice, n, res);
        // 回退
    }
}

/* 爬楼梯：回溯 */
int climbingStairsBacktrack(int n) {
    vector<int> choices = {1, 2}; // 可选择向上爬 1 阶或 2 阶
    int state = 0;                // 从第 0 阶开始爬
    vector<int> res = {0};        // 使用 res[0] 记录方案数量
    backtrack(choices, state, n, res);
    return res[0];
}

方法一：暴力搜索

回溯算法通常并不显式地对问题进行拆解，而是将求解问题看作一系列决策步骤，通过试探和剪枝，搜索所有可能的解。

我们可以尝试从问题分解的角度分析这道题。设爬到第 i 阶共有 dp[i] 种方案，那么 dp[i] 就是原问题，其子问题包括：

dp[i − 1], dp[i − 2], …, dp[2], dp[1]

由于每轮只能上 1 阶或 2 阶，因此当我们站在第 i 阶楼梯上时，上一轮只可能站在第 i − 1 阶或第 i − 2 阶上。换句话说，我们只能从第 i − 1 阶或第 i − 2 阶迈向第 i 阶。

由此便可得出一个重要推论：爬到第 i − 1 阶的方案数加上爬到第 i − 2 阶的方案数就等于爬到第 i 阶的方案数。公式如下：

dp[i] = dp[i − 1] + dp[i − 2]

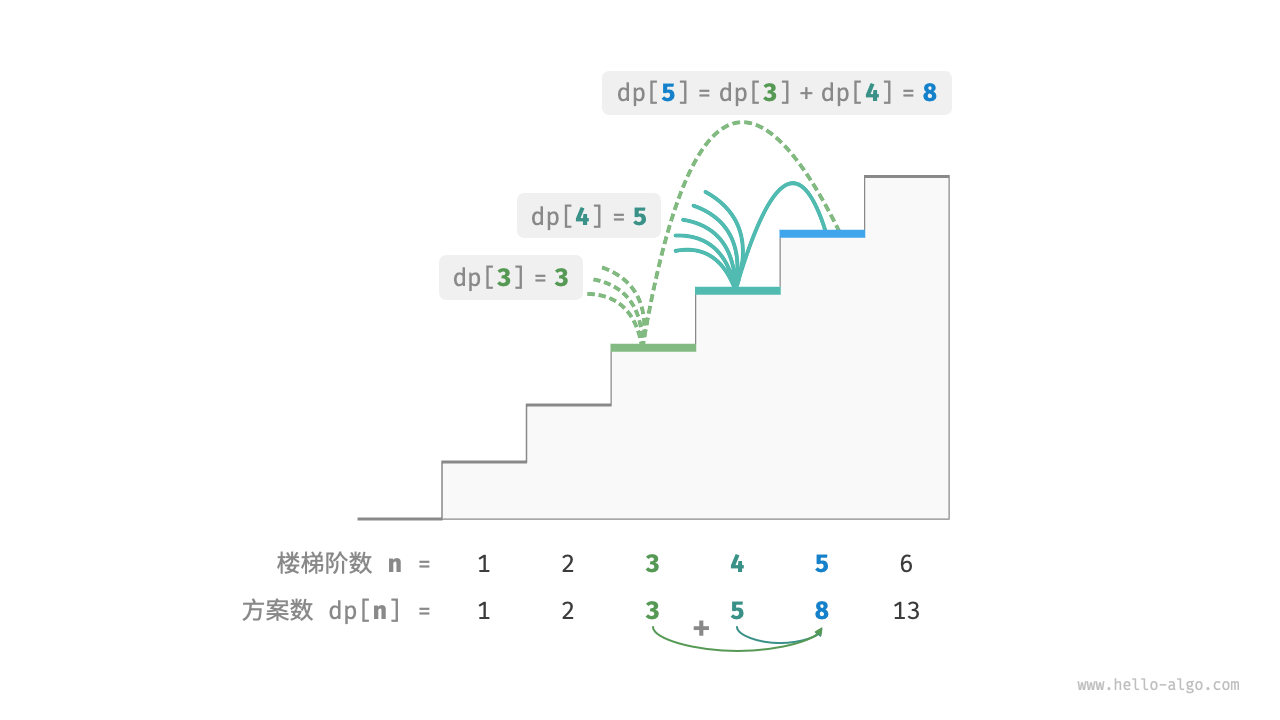
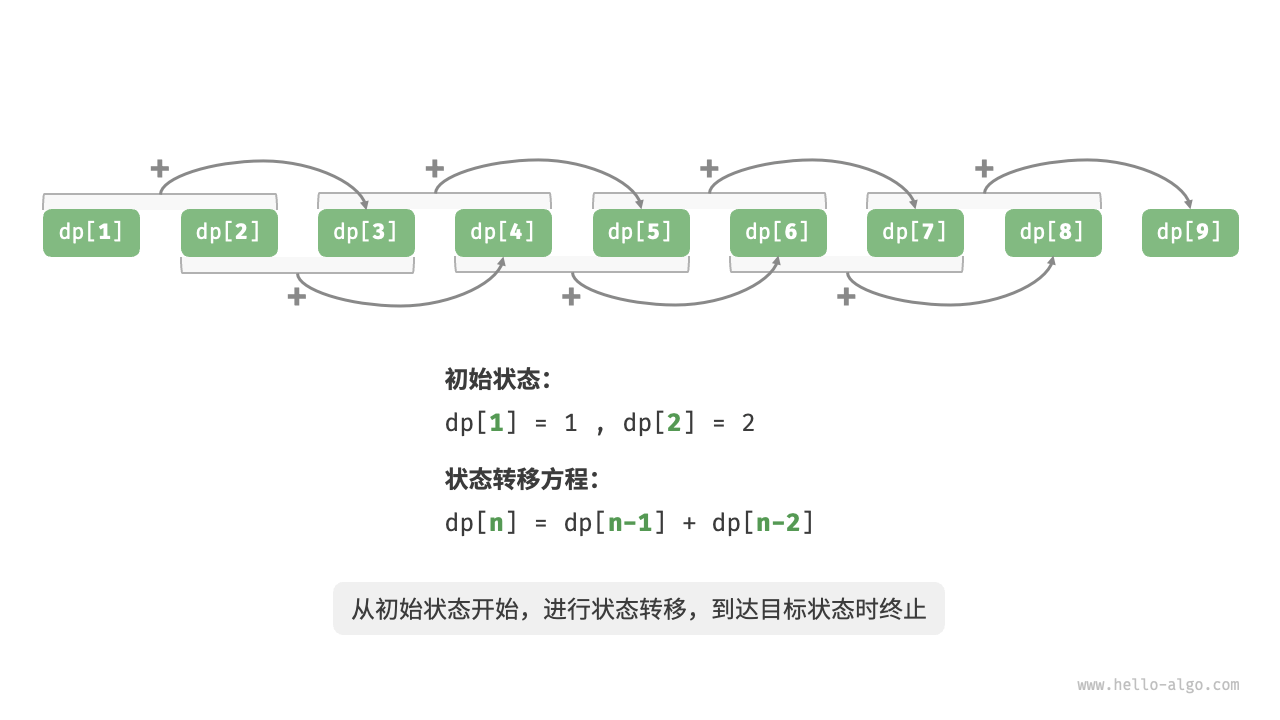
这意味着在爬楼梯问题中，各个子问题之间存在递推关系，原问题的解可以由子问题的解构建得来。下图展示了该递推关系。

我们可以根据递推公式得到暴力搜索解法。以 dp[n] 为起始点，递归地将一个较大问题拆解为两个较小问题的和，直至到达最小子问题 dp[1] 和 dp[2] 时返回。其中，最小子问题的解是已知的，即 dp[1] = 1、dp[2] = 2 ，表示爬到第 1、2 阶分别有 1、2 种方案。

观察以下代码，它和标准回溯代码都属于深度优先搜索，但更加简洁：

/* 搜索 */
int dfs(int i) {
    // 已知 dp[1] 和 dp[2] ，返回之
    if (i == 1 || i == 2)
        return i;
    // dp[i] = dp[i-1] + dp[i-2]
    int count = dfs(i - 1) + dfs(i - 2);
    return count;
}

/* 爬楼梯：搜索 */
int climbingStairsDFS(int n) {
    return dfs(n);
}

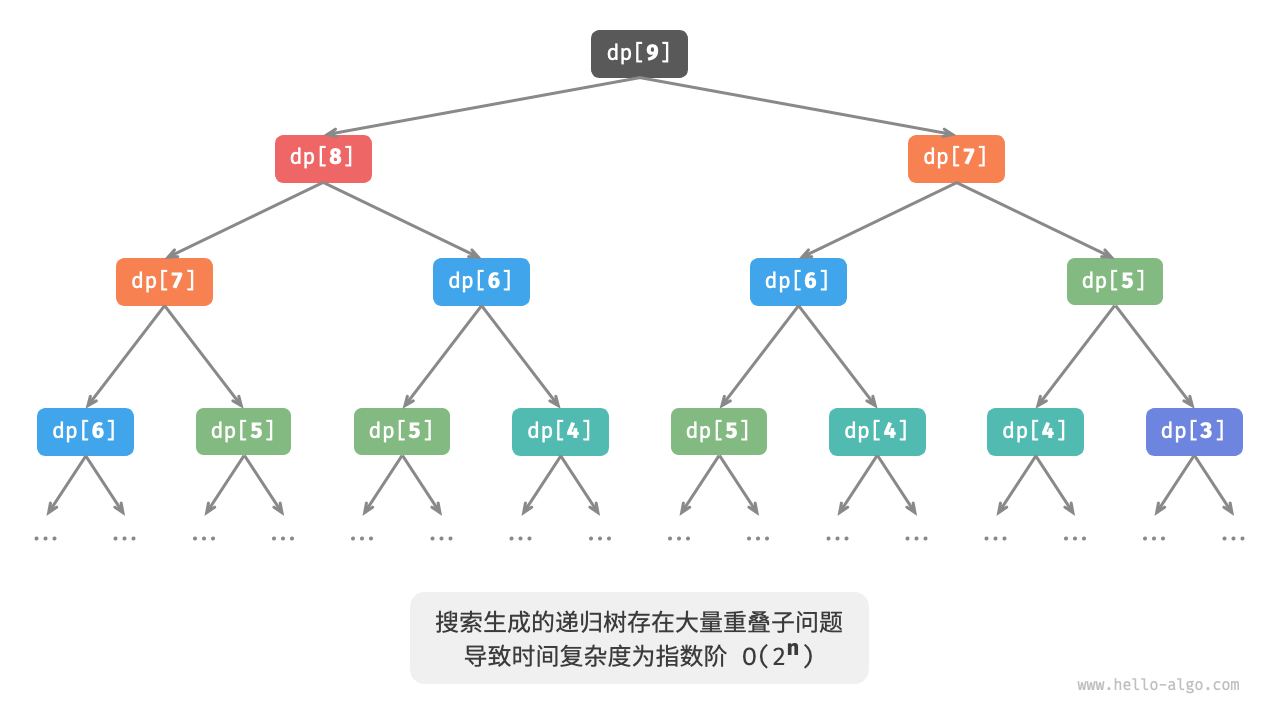
下图展示了暴力搜索形成的递归树。对于问题 dp[n] ，其递归树的深度为 n ，时间复杂度为 O(2ⁿ) 。指数阶属于爆炸式增长，如果我们输入一个比较大的 n ，则会陷入漫长的等待之中。

观察上图，指数阶的时间复杂度是“重叠子问题”导致的。例如 dp[9] 被分解为 dp[8] 和 dp[7] ，dp[8] 被分解为 dp[7] 和 dp[6] ，两者都包含子问题 dp[7] 。

以此类推，子问题中包含更小的重叠子问题，子子孙孙无穷尽也。绝大部分计算资源都浪费在这些重叠的子问题上。

方法二：记忆化搜索

为了提升算法效率，我们希望所有的重叠子问题都只被计算一次。为此，我们声明一个数组 mem 来记录每个子问题的解，并在搜索过程中将重叠子问题剪枝。

当首次计算 dp[i] 时，我们将其记录至 mem[i] ，以便之后使用。
当再次需要计算 dp[i] 时，我们便可直接从 mem[i] 中获取结果，从而避免重复计算该子问题。

代码如下所示：

/* 记忆化搜索 */
int dfs(int i, vector<int> &mem) {
    // 已知 dp[1] 和 dp[2] ，返回之
    if (i == 1 || i == 2)
        return i;
    // 若存在记录 dp[i] ，则直接返回之
    if (mem[i] != -1)
        return mem[i];
    // dp[i] = dp[i-1] + dp[i-2]
    int count = dfs(i - 1, mem) + dfs(i - 2, mem);
    // 记录 dp[i]
    mem[i] = count;
    return count;
}

/* 爬楼梯：记忆化搜索 */
int climbingStairsDFSMem(int n) {
    // mem[i] 记录爬到第 i 阶的方案总数，-1 代表无记录
    vector<int> mem(n + 1, -1);
    return dfs(n, mem);
}

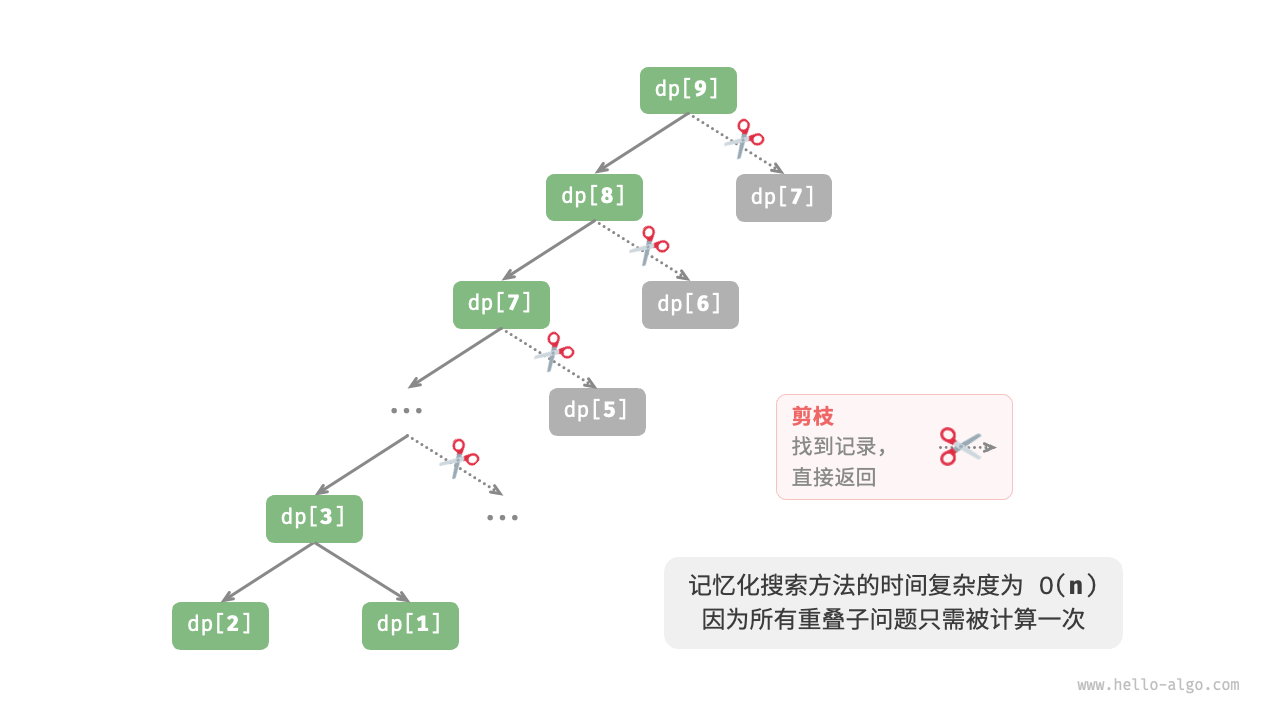
观察下图，经过记忆化处理后，所有重叠子问题都只需计算一次，时间复杂度优化至 O(n) ，这是一个巨大的飞跃。

方法三：动态规划

记忆化搜索是一种“从顶至底”的方法：我们从原问题（根节点）开始，递归地将较大子问题分解为较小子问题，直至解已知的最小子问题（叶节点）。之后，通过回溯逐层收集子问题的解，构建出原问题的解。

与之相反，动态规划是一种“从底至顶”的方法：从最小子问题的解开始，迭代地构建更大子问题的解，直至得到原问题的解。

由于动态规划不包含回溯过程，因此只需使用循环迭代实现，无须使用递归。在以下代码中，我们初始化一个数组 dp 来存储子问题的解，它起到了与记忆化搜索中数组 mem 相同的记录作用：

/* 爬楼梯：动态规划 */
int climbingStairsDP(int n) {
    if (n == 1 || n == 2)
        return n;
    // 初始化 dp 表，用于存储子问题的解
    vector<int> dp(n + 1);
    // 初始状态：预设最小子问题的解
    dp[1] = 1;
    dp[2] = 2;
    // 状态转移：从较小子问题逐步求解较大子问题
    for (int i = 3; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];
}

下图模拟了以上代码的执行过程。

与回溯算法一样，动态规划也使用“状态”概念来表示问题求解的特定阶段，每个状态都对应一个子问题以及相应的局部最优解。例如，爬楼梯问题的状态定义为当前所在楼梯阶数 i 。

根据以上内容，我们可以总结出动态规划的常用术语。

将数组 dp 称为 dp 表，dp[i] 表示状态 i 对应子问题的解。
将最小子问题对应的状态（第 1 阶和第 2 阶楼梯）称为初始状态。
将递推公式 dp[i] = dp[i − 1] + dp[i − 2] 称为状态转移方程。

空间优化

细心的读者可能发现了，由于 dp[i] 只与 dp[i − 1] 和 dp[i − 2] 有关，因此我们无须使用一个数组 dp 来存储所有子问题的解，而只需两个变量滚动前进即可。代码如下所示：

/* 爬楼梯：空间优化后的动态规划 */
int climbingStairsDPComp(int n) {
    if (n == 1 || n == 2)
        return n;
    int a = 1, b = 2;
    for (int i = 3; i <= n; i++) {
        int tmp = b;
        b = a + b;
        a = tmp;
    }
    return b;
}

观察以上代码，由于省去了数组 dp 占用的空间，因此空间复杂度从 O(n) 降至 O(1) 。

在动态规划问题中，当前状态往往仅与前面有限个状态有关，这时我们可以只保留必要的状态，通过“降维”来节省内存空间。这种空间优化技巧被称为“滚动变量”或“滚动数组”。